Maestría en Ingeniería Mecatrónica

Seminario de Investigación  

Docente: Dr. David Ricardo López Flores

Correo: david.lf@chihuahua.tecnm.mx

Carrera: Doctorado en Ingenieria

Clave de la asignatura: D1D

Division de Estudios de Postgrado e Investigación

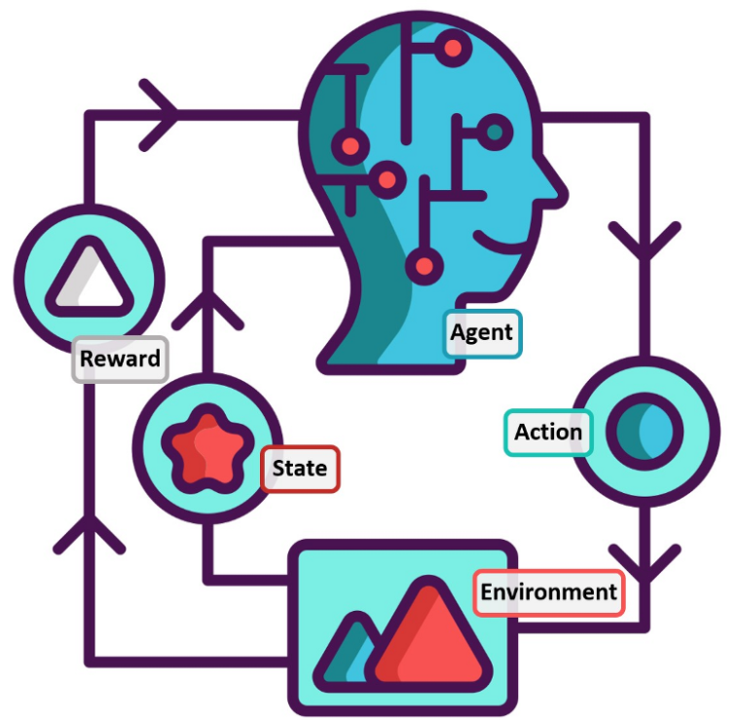
El aprendizaje por reforzamiento es aprender qué hacer, cómo mapear situaciones en acciones, para maximizar una señal de recompensa numérica. Al aprendiz no se le dice qué acciones tomar, sino que debe descubrir qué acciones producen la mayor recompensa al probarlas. En los casos más interesantes y desafiantes, las acciones pueden afectar no sólo la inmediata recompensa, sino también la siguiente situación y, a través de ella, todas las recompensas subsiguientes. Estas dos características (búsqueda por prueba y error y recompensa retrasada) son las dos más importantes características distintivas del aprendizaje por refuerzo.

Formalizamos el problema del aprendizaje por refuerzo usando ideas de la teoría de sistemas dinámicos, específicamente, como el control óptimo de procesos de decisión de Markov incompletamente conocidos. La idea básica es capturar los aspectos más importantes del problema real que enfrenta un agente de aprendizaje que interactúa a lo largo del tiempo con su entorno para lograr un objetivo. Un agente de aprendizaje debe ser capaz de sensar el estado de su entorno hasta cierto punto y debe ser capaz de emprender acciones que afecten al estado. El agente también debe tener metas relacionadas con el estado del medio ambiente. Los procesos de decisión de Markov pretenden incluir solo estos tres aspectos -sensado, acción y meta- en sus formas más simples posibles sin banalizar a cualquiera de ellos. Cualquier método que sea adecuado para resolver tales problemas se considera como un método de aprendizaje por refuerzo.

Supervisión del Proyecto de Tesis

• La asignatura contribuye a desarrollar el pensamiento lógico, matemático y estructurado al perfil del Maestro en Ingeniería y le aporta herramientas básicas para desarrollar soluciones abstractas y concretas a problemas de Ingeniería en general, y de Mecatrónica en particular, mediante la implementación de aplicaciones y sistemas de software.
• Proporciona herramientas que permiten modelar fenómenos de contexto, al crear modelos computacionales e implementaciones que recurren a metodologías matemáticas formales como el Cálculo Integral, Cálculo Diferencial, Ecuaciones Diferenciales, Cálculo Vectorial y Matemáticas Discretas y asignaturas de Física y Ciencias de la Ingeniería, por lo que permite diseñar proyectos integradores con cualquiera de ellas.
• La característica más sobresaliente de esta asignatura es que en ella se estudian las bases sobre las cuales se construyen las Ciencias Computacionales, componente medular de la Mecatrónica.